DISTRIBUSI PELUANG KONTINU

PENDAHULUAN

LATAR BELAKANG

Bila kita mengingat kembali pengetahuan mengenai data yang dikelompokkan menjadi bentuk tabel distribusi frekuensi. Kita telah mengetahui bahwa dengan tabel distribusi frekuensi itu kita dapat membuat histogram, poligon, ogif dan menentukan frekuensi kemiringan suatu distribusi data.
Perhatikan bahwa dari poligon kita dapat melukis suatu kurva yang halus dan kontinu, yaitu grafik dari fungsi f(x). Dari kurva ini kita dapat menentukan bagaimana kemiringan dari suatu distribusi data. Dari kemiringan tersebu, kita dapat mengetahui bahwa ada tiga jenis kemiringan, yaitu miring ke kiri, simetri, dan miring ke kanan. Dan dari jenis kemiringan tersebut, kita akan mengetahui jenis-jenis dan intepretasi  dari distribusi kontinu, yaitu distribusi normal, chi-kuadrat, distribusi F, dan distribusi t ?


RUMUSAN MASALAH

1. Apa pengertian distribusi normal, chi-kuadrat, distribusi F, dan distribusi t ?
2. Apa persamaan umum dari distribusi normal, chi-kuadrat, distribusi F, dan distribusi t ?

PEMBAHASAN

DISTRIBUSI NORMAL

Dikenalnya distribusi normal diawali oleh kemajuan yang pesat dalam pengukuran pada abad ke 19. Pada waktu itu, para ahli matematika dihadapkan pada suatu tantangan mengenai fenomena variabilitas pengamat atau interna yang artinya bila seorang mengadakan pengukuran berulang-ulang maka hasilnya akan berbeda-beda.

Yang menjadi pertanyaan adalah nilai manakah yang dianggap paling tepat dari semua hasil pengukuran tersebut. Maka kemudian berdasarkan kesepakatan maka nilai rata-rata dianggap paling tepat dan semua penyimpangan dari rata-rata dianggap suatu kesalahan atau error.
Abraham de Moivre adalah yang pertama kali memperkenalkan distribusi normal ini dan kemudian dipopulerkan oleh Carl Fredreich Gauss. Sehingga nama lain distribusi ini adalah distribusi Gauss.

Ciri-ciri distribusi normal

Distribusi normal mempunyai beberapa sifat dan ciri, yaitu:

• Disusun dari variable random kontinu
• Kurva distribusi normal mempunyai satu puncak (uni-modal)
• Kurva berbentuk simetris dan menyerupai lonceng hingga mean, median dan modus terletak pada satu titik.
• Kurva normal dibentuk dengan N yang tak terhingga.
• Peristiwa yang dimiliki tetap independen.
• Ekor kurva mendekati absis pada penyimpangan 3 SD ke kanan dan ke kiri dari rata-rata dan ekor grafik dapat dikembangkan sampai tak terhingga tanpa menyentuh sumbu absis.

Distibusi normal standar

Suatu distribusi normal tidak hanya memiliki satu kurva, tetapi merupakan kumpulan kurva yang mempunyai ciri-ciri yang sama.sehingga harus ditentukan 1 pegangan sebagai distribusi nprmal yang standar.

Ada 2 cara untuk menentukan distribusi normal :

1. cara ordinat:
Menggunakan rumus distribusi normal berikut :



µ = rata-rata
σ   = simpang baku
π = 3,1416 (bilangan konstan)
e = 2,7183 (bilangan konstan)
X = absis dengan batas -∞ < X < π

Bila nilai µ dan σ tetap maka setiap nilai x akan menghasilkan nlai y sehingga bila nilai x dimasukkan dalam perhitungan berkali-kali dengan julah tak terhingga maka akan dihasilkan suatu kurva distribusi normal. Terdapat banyak kurva  normal dengan bentuk yang berlainan, tergantung dari besar dan kecilnya σ.

Bila σ besar, kurva yang terbentuk mempunyai puncak yang rendah, sebaliknya bila σ kecil akan menghasilkan puncak kurva yang tinggi.
Dapat pula bentuk kurva normal dengan µ yang  berbeda atau dengan µ dan σ yang berbeda

2. Cara luas
Kurva normal adalah kurva yang simetris, yang berarti bahwa kurva ini akan membagi luas kurva  menjadi 2 bagian yang sama.Seluruh luas kurva = 1 atau 100% dan rata-rata (µ) membagi luas kurva menjadi 2 bagian yang sama. Berarti luas tiap belahan adalah 50%. Setiap penyimpangan rata-rata dapat ditentukan presentase terhadap seluruh luas kurva. Penyimpangan ke kanan dan ke kiri :
-.penyimpangan  1 SD = 68,2% dari seluruh luas kurva.
-.penyimpangan 2 SD = 95,5% dari seluruh luas kurva.
-.penyimpangan 3 SD, = 99,7% dari seluruh luas kurva.



Proses standarisasi dapat dilakukan dengan transformasi rumus (kurva normal standar) :

            Z = x - µ
                     σ

      x = nilai variable random
µ = rata-rata distribusi
σ = simpang baku
Z = nilai standar, yaitu besarnya penyimpangan suatu nilai terhadap  rata-rata yang dinyatakan dari unit SD.

Standarisasi penting dilakukan karena ada variabel random yang memiliki satuan yang berbeda-beda, seperti cm, kg, bulan.
Untuk memudahkan perhitungan dapat digunakan sebuah table yang menunjukkan luas area di bawah kurva normal antara nilai rata-rata dan suatu nilai variable random yang dinyatakan dalam unit SD.

Misalnya : luas 95% adalah 1,96 SD.
Untuk transformasi distribusi normal menjadi distribusi normal  standar dinyatakan  µ = 0 dan σ = 1.

Penggunaan tabel distribusi normal

Tabel distribusi normal standar terdiri dari kolom dan baris. Kolom paling kiri menunjukkan nilai Z, tertera angka 0 sampai 3 dengan satu desimal dibelakangnya. Desimal berikutnya terletak pada baris paling atas dengan angka dari 0 sampai 9.
Misalnya dari hasil perhitungan diperoleh nilai Z = 1,96
Maka di kolom kiri kita cari nilai1,9 dan baris atas kita cari angka 6
Dari kolom 6 bergarak ke bawah, hingga pertemuan titik yang menunjukkan angka 0,4750.
Berarti luas daerah di dalam kurva normal antara rata-rata dengan 1,96 SD ke kanan adalah 0,475.
Karena luas kurva ke kanan dan ke kiri sama, maka luas penyimpangan 1,96 ke kanan dan ke kiri dari rata-rata adalah 0,95 (95%).

Aplikasi distribusi normal

Sebagai contoh aplikasi distribusi normal, dilakukan suatu evaluasi thd pengobatan TB menggunakan Rifampicin dengan rata-rata kesimpulan 200 hari dan standar deviasinya sebesar 10. Berapakah probabilitas kesembuhan antara 190 dan 210?
 Jawab :
     Mula-mula dihitung nilai Z =210
     Z= (210-200)/10 = 1=0,3413
     jadi probabilitas kesembuhan 190 sampai 210 = 0,3413+0,3413=0,6826=68,26

Contoh penggunaan:
Hitung P (X<1 br="">
Penyelesaian:

1,25 = 1,2 + 0,05 maka pada tabel, carilah angka 1,2 pada kolom paling kiri. Selanjutnya, carilah angka 0,05 pada baris paling atas. Sel pada pertemuan kolom dan baris tersebut adalah 0,8944.
Dengan demikian, P (X<1 0="" adalah="" o:p="">

DISTRIBUSI T – STUDENT  ( DISTRIBUSI T )

Untuk sampel nukuran n   3, taksiran σ^2 dapat diperoleh dengan menghitung nilai S2. Bila n   30, maka S2 memberikan taksiran σ^2 yang baik dan tidak berubah dan distribusi statistik ((X ̅-μ))⁄((S⁄√n)) masih secara hampiran, berdistribusi sama dengan peubah normal baku z.
Bila ukuran sampel  ( n < 30 ), nilai S2 berubah cukup besar  dari sampel ke sampel dan distribusi peubah acak ((X ̅-μ))⁄((S⁄√n))  tidak lagi distribusi normal baku.
Dalam hal ini didapatkan distribusi statistik yang disebut T


Distribusi sampel  T di dapat  dari anggapan bahwa sampel acak berasal dari populasi normal.
T=(((X ̅-μ))⁄((σ⁄(√n))))/√(S^2⁄σ^2 )=Z/√(V(n-1))
Dengan ,
Z=(X ̅-μ)/(σ⁄√n)
Berdistribusi normal baku,dan
V=((n-1) S^2)/σ^2

Misalkan Z peubah acak normal baku dan V peubah acak khi-kuadrat dengan derajat kebebasan v. Bila z dan v bebas, maka distribusi peubah acak T, bila


Diberikan oleh,




Ini di kenal dengan nama distribusi t dengan derajat kebebasan v.
Distribusi Z dan T berbeda karena variansi T bergantung pada ukuran sampel n dan variansi ini selalu lebih besar dari 1. Hanya bila ukuran sampel n→∞ kedua distribusi menjadi sama. Pada gambar dibawah diperlihatkan hubungan antara distribusi normal baku (v=∞) dan distribusi t untuk derajat kebebasan 2 dan 5.












Karena distribusi t setangkup terhadap rataan nol, maka t_(1-α)=〖-t〗_α; yaitu, nilai t yang luas sebelah kanannya 1-α, atau luas sebelah kirinya α, sama dengan minus nilai t yang luas bagian kanannya α.
Panjang selang nilai t yang dapat diterima tergantung pada bagaimana pentingnya μ. Bila μ ingin ditaksir dengan ketelitian yang tinggi, sebaiknya digunakan selang yang lebih pendek seperti 〖-t〗_0,05 sampai t_0,05.


   Contoh soal

Suatu pabrik bola lampu yakin bahwa bola lampunya akan tahan menyala rata – rata selama 500 jam. Untuk mempertahankan nilai tersebut, tiap bulan diuji 25 bola lampu. Bila  nilai t yang dihitung terletak antara 〖-t〗_0,05 dan t_0,05 maka pengusahan pabrik tadi akan mempertahankan kenyakinannya. Kesimpulan apa yang seharusnya dia ambil dari sampel dengan rataan x ̅  = 518 jam dan simpangan baku s = 40 jam? Anggap bahwa distribusi waktu menyala, secara hampiran, noramal.

Jawab :

Dari tabel 5 diperoleh t_0,05 = 1,711 untuk derajat kebebasan 24. Jadi pengusaha tadi akan puas dengan keyakinananya bila sampel 25 bola lampu memberikan nilai t antara -1,711 dan 1,711. Bila memang μ = 500, maka
t=(518-500)/(40/√25)=2,25

Suatu nilai yang cukup jauh di atas 1,711. Peluang mendapat nilai t, dengan derajat kebebasan v = 24, sama atau lebih besar dari 2,25, secara hampiran adalah 0,02. Bila μ>500, nilai t yang di hitung dari sampel akan lebih wajar. Jadi pengusaha tali kemungkinan besar akan menyimpilkan bahwa produksinya lebih nbaik daripada yang diduganya semula.

Distribusi F

Statistik F didefinisikan sebagai nisbah dua peubah acak khi-kuadrat yang bebas, masing – masing dibagi dengan derajat kebebasannya. Misalkan U dan V dua peubah acak bebas masing – masing berdistribusi khi-kuadrat dengan derajat kebebasan v_1  dan v_2. Maka distribusi peubah acak :





Diberikan oleh







ini dikenal dengan nama distribusi F dengan derajat kebebasan v_1 dan v_2
Kurva distribusi F tidak hanya tergantung pada kedua parameter  v_1 dan v_2  tapi juga pada urutan keduanya ditulis.begitu kedua bilangan itu ditentukan maka kurvanya menjadi tertentu. Dibawah ini adalah kurva khas distribusi F











Di bawah ini gambar kurva nilai tabel distribusi F











Lambang  f_α nilai  f  tertentu peubah acak F sehingga disebelah kanannya terdapat luas sebesar α. Ini digambarkan dengan daerah  yang dihitami pada gambar 2. Pada tabel  memberikan nilai f_α hanya untuk α=0,05 dan α=0,01 untuk berbagai pasangan derajat kebebasan v_1 dan v_2 Jadi, nilai f untuk derajat kebebasan 6 dan 10 , sehingga luas daerah sebelah kanannya 0,05 adalah f_0,05=3,22.

Tulislah f_α (v_1,v_2) untuk f_α dengan derajat kebebasan v_1 dan v_2, maka





Bila S_1^2 dan S_2^2 variansi sampel acak ukuran n_1 dan n_2 yang diambil dari dua populasi normal, masing-masing dengan variansi σ_1^2 dan σ_2^2, maka





Berdistribusi F dengan derajat kebebasan v_1=n_1-1 dan v_2=n_2-1

   Contoh :
Tentukan nilai dari F 0,05 (12,20)
Penyelesaian  :
Diketahui :
 p = 0,05
V_1=12 , V_2=20
Ditanya : F = . . . . ?

Jawab :
F 0,05 (12,20) = 2,28
P = 1 – 0,05 = 0,95
F 0,95 (20,12) = 1/(F0,05(12,20))=1/2,28=0,04
Jadi nilai F 0,05 (12,20) adalah 0,04

       Distribusi chi kuadrat

Dalam menganalisis uji statistik yang menggunakan distribusi chi-squared tentu saja perlu adanya perbandingan dengan batas untuk memutuskan apakah hipotesisnya diterima atau tidak. Untuk itu perlu adanya tabel chi-square yang bisa memutuskan hasil dari analisis. Berikut contoh batasan dari distribusi chi-square

Pada area hitam diatas merupakan daerah tolak hipotesis sedangkan yang putih untuk keputusan terima hipotesis awal. Garis pemisah antar dua daerah tersebut adalah gambaran dari tabel chi-square.

Bagian-bagian dari tabel chi-squared :

1.             Titik kritis (alpha), merupakan nilai peluang dari tingkat kesalahan yang dapat diterima. Nilai yang sering digunakan yaitu 0.05 (5%). nilai ini ditentukan oleh peneliti sebelumnya.

2.             Degree of freedom (df), atau derajat kebebasan. menentukan nilai degree of freedom ini berbeda-beda tiap metode yang digunakan. tapi umumnya jumlah sampel(n)-1.

3.             Nilai tabel chi-square. Merupakan nilai batas tolak atau terima hipotesis awal. Inilah yang akan dicari

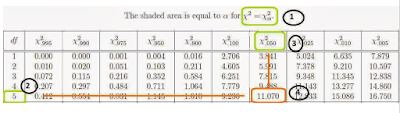
Cara membaca tabel chi-sqaured

Dalam menguji tabel chi-squared dengan alpha 5% dan derajat bebas 5 tertulis seperti berikut. (0.05,5). Agar lebih jelas dalam membaca tabel chi-square gunakan gambar seperti berikut ini:

Penjelasan gambar tabel :

1.         Menjelaskan jenis dari tabel chi-square. terlihat bahwa ada tulis alpha menunjukkan bahwa tabel chi-square dengan titik kritis alpha.

2.         Kolom df. yang menunjukkan nilai df yang digunakan. contohnya yaitu5.

3.         Baris Alpha, menujukkan alpha yang digunakan. Jangan terkecoh dengan angka tersebut sesuai kan dengan jenis tabel seperti pada nomor 1.

4.         Nilai chi-square tabel, nilai ini lah yang dicari. caranya sangat mudah yaitu menghubungkan antar kolom df dan baris alpha yang digunakan seperti pada gambar diatas.

Contoh :

Misalnya kita memperoleh nilai statistik uji chi-square = 11,111 dari rumus yang digunakan atau software. kemudian dibandingkan dengan nilai tabel chi-square yang diperoleh diatas yaitu 11.070. Karena nilai uji stat  chi-square lebih besar dari nilai tabel chi-square. maka keputusan tolak H0. sebaiknya jika lebih kecil dari tabel chi-square maka keputusan terima H0. jika diilustrasikan dengan gambar diatas maka nilainya berada di daerah hitam. karena nilai tabel berada dibatas tersebut dan nilai uji stat lebih besar sehingga melewati batas tersebut.

DAFTAR PUSTAKA

Statistikdasar.com

http://keepcopying.blogspot.com/2013/12/distribusi-probabilitas-kontinu.html

http://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=1&cad=rja&uact=8&ved=0CB4QFjAA&url=http%3A%2F%2Fopenwetware.org%2Fimages%2Fc%2Fc8%2FMakalah_distribusi_probabilitas-normal-sampling.doc&ei=9_YpVezgIo--uASEtYCADA&usg=AFQjCNHoK5ap8olrwbDuVtAiCIJjZ_vFmw&sig2=A41o7iJ265Cl_Dr20jMdVQ

https://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=2&cad=rja&uact=8&ved=0CCYQFjAB&url=https%3A%2F%2Fliliasinta.files.wordpress.com%2F2011%2F01%2Fdistribusi-t.docx&ei=fvcpVYvJIsKzuASC2IGQDQ&usg=AFQjCNF2SFBCZdhDDb1qyLftZJGjMt7kAw&sig2=2lRrhTbArJPcz2zDDea8Gw